Lý thuyết cơ bản về tính toán rung xóc (rung động)

Rung xóc (rung động) là một dạng của chuyển động, với mối tương quan giữa gia tốc, tốc độ và độ dịch chuyển (biên độ). Để mô tả rung động (rung xóc), các đơn vị này thường được sử dụng. 

Nội dung

---

Các đại lượng (thông số) cơ bản sử dụng trong thử nghiệm rung xóc

Có bốn đại lượng quan trọng:

-  Lực (N)   

-  Gia tốc (m/s²)     

-  Tốc độ (m/s)  

-  Độ dịch chuyển (biên độ) (mm_p-p)

Công thức tính tính toán rung xóc (rung động)

F = mA		Đơn vị SI	Đơn vị trong hệ kỹ thuật
	F: lực	N	Kgf
	m: khối lượng	Kg	Kg
	A: gia tốc	m/s2	G

• Theo đó, nếu vật có khối lượng 1kg gia tốc tới 1m/s² thì cần một lực 1N. Gia tốc trọng trường G bằng 9.8m/s²
• Để mô tả rung xóc (rung động) thì tần số và biên độ cần phải xác định. Rung động là một dạng của chuyển động, với mối tương quan giữa gia tốc, tốc độ và độ dịch chuyển (biên độ). Để mô tả rung xóc (rung động), các đơn vị này đều có thể được sử dụng. Dưới đây là mối tương quan giữa các đơn vị này.

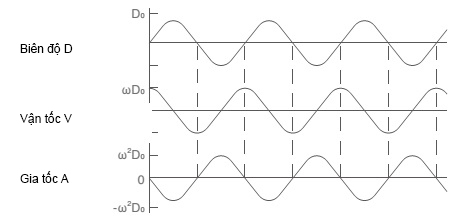
Giả sử chúng ta có một vật chuyển động theo hình sine

Độ dịch chuyển (quãng đường di chuyển)

                           D=D₀sinωt

Vận tốc thì bằng đạo hàm của độ dịch chuyển (biên độ). Do đó:

                          V  = dD/dt

                          V  = ꞷD₀cosꞷt

Gia tốc thì bằng đạo hàm của vận tốc

                          A  = dV/dt

                          A  = -ꞷ²D₀sinꞷt

Ngoài ra

                         ω=2πft

Chúng ta có được các hàm với biến là biên độ

                   V = ꞷD = 2ᴨfD                 D - khoảng cách (m)           A - gia tốc (m/s²)

                   A  = ꞷ²D=  (2ᴨf)²D            V - vận tốc (m/s)

Chúng ta có được các hàm dưới đây bằng cách biến đổi các hàm bên trên:

                       f  = A/2πV                     V = ꞷD = 2ᴨfD         

                       A  = V²/D                       D = A/(2πf)²

• Trong thử nghiệm rung xóc, chúng ta sử dụng biên độ dịch chuyển (mm_p-p)

            Do đó:

                            D  = d/2000         

• Thay vào tất cả các hàm bên trên

                           f = A/2ᴨV                         f - tần số (Hz)

                          A= (2ᴨf)²d/2000               A  - gia tốc (m/s²)

                          V = 2ᴨfd/2000                  V - vận tốc (m/s)

                          d = 2000A/(4ᴨ²)f              d - khoảng cách (mm)

           Ví dụ:

                         f = 50Hz;  d= 2mm

                         V = 2ᴨfd/2000=  = 2ᴨ.50.2/2000  = 0.314  m/s

                         A= (2ᴨf)²d/2000  =  (2ᴨ50)²2/2000  = 98.7 m/s²

Khái niệm dB

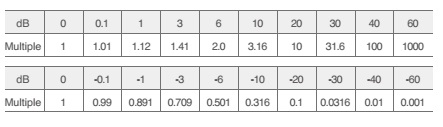
Chúng ta sử dụng đơn vị dB khi mô tả mối tương quan giữa các đại lượng vật lý. Đặc biệt trong trường hợp khi một giá trị là một bội hàng nghìn hoặc triệu lần của giá trị tương ứng, khi đó chúng ta sử dụng thang logarit thay cho thang tuyến tính. Điều này giúp dễ hình dung các giá trị hơn và là một tiêu chuẩn kiểm tra công nghiệp

             dB được diễn tả theo bên dưới:

                           a = 20 log(A1/A0) [dB]                      

             Một triệu lần bằng

                           a = 20 log (1000 000/1) = 120 [dB]

• Đơn vị dB không chỉ giảm số lượng số cần dùng mà còn đơn giản hóa phép tính. Ví dụ, 25dB cộng 30dB bằng 55dB nhưng nếu tính theo thang tuyến tính:

                            25dB = 20 log A                  A = 1025/20=17.78

                            30dB = 20 log B                  B = 1030/20=31.62

                            AxB = 17.78×31.62=562.3=20 log 562.3 = 55dB

• Giờ chúng ta có thể sử dụng phép cộng thay cho phép nhân bằng cách sử dụng dB. Hay nói cách khác sử dụng dB rất dễ để tính toán. Dưới đây là bảng chuyển đổi giữa dB và bội số của dB.  

  

Sử dụng đồ thị logarit

• Chúng ta thường sử dụng đồ thị logarit khi cần vẽ dữ liệu của kiểm tra độ rung hoặc các hiện tượng vật lý khác

              

• Trên đồ thị tuyến tinh chúng ta có thể xác định Y=20 khi X=100. Nhưng chúng ta khó có thể xác định Y khi X bằng 10 hoặc 1. Trên đồ thị logarit chúng ta có thể xác định giá trị ngay cả khi X là 1/100 hay 1/1000. Do đó sử dụng đồ thị logarit tiện lợi hơn nhiều

Đồ thị thử nghiệm dạng hình sine

• Chúng ta thường sử dụng đồ thị bên dưới khi thử nghiệm rung xóc dạng hình sine. Đây là đồ thị log-log đã được đề cập bên trên. Tiệm cận của gia tốc, vận tốc và hoán vị cố định được thể hiện trên đồ thị. Dưới đây là một ví dụ về tiệm cận của tốc độ không đổi. Từ các hàm chúng ta biết trước

                                A = (2ᴨf) V         A - gia tốc; f - tần số; V - vận tốc

• Phương trình này cho thấy gia tốc A tăng 100 lần khi tần số f tăng 10 lần. Trên đồ thị bên dưới, chúng ta có thể thấy gia tốc tăng từ 1m/s² tới 100m/s² khi tần số tăng từ 1Hz tới 10Hz

                                  A =  (2ᴨf)²D            D - khoảng cách (biên độ)

>>> XEM THÊM CÁC SẢN PHẨM THIẾT BỊ THỬ NGHIỆM >>>

Tủ thử nghiệm nhiệt độ, độ ẩm

Tủ thử nghiệm sốc nhiệt

Máy thử rung xóc

Tủ thử nghiệm phun sương muối

Tủ thử nghiệm nhiệt độ, áp suất theo độ cao

Tủ thử nghiệm chống xâm nhập IPx

Thiết bị thử nghiệm rơi và va đập

Thiết bị thử nghiệm NVH

======================

VintechME - 1Tech Việt Nam là đơn vị chuyên cung cấp các giải pháp kỹ thuật toàn diện bao gồm trang thiết bị và các gói dịch vụ liên quan đến thử nghiệm, đo lường.
Hotline (Zalo/ Whatsaap): 0966 252 565/ 0979 388 908/ 0972 317 221
Email: info@vintechme.com
Fanpage: https://www.facebook.com/vintechme
Website: https://vintechme.com/
Địa chỉ: Số 197, đường Thụy Phương, Bắc Từ Liêm, Hà Nội, Việt Nam.